[Python] 백준 9095_1, 2, 3 더하기 (DP 문제)
2023. 3. 19. 17:19ㆍ알고리즘
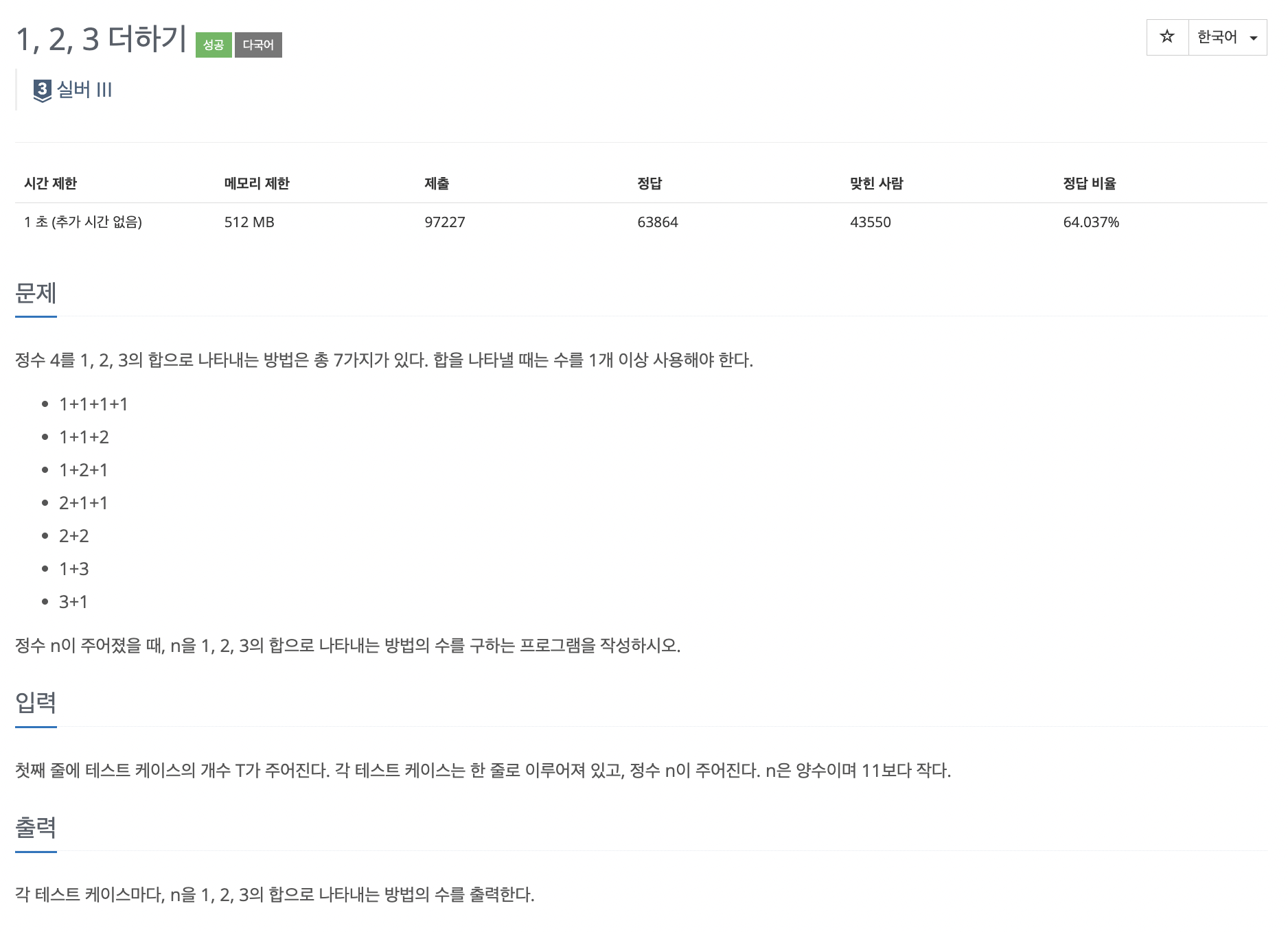
Dynamic Programming 문제다. 규칙을 찾으면 된다!
- 1 를 1, 2, 3의 합으로 나타내는 방법의 수 = 1 (1가지)
- 2 를 1, 2, 3의 합으로 나타내는 방법의 수 = 1 + 1, 2 (2가지)
- 1의 합으로 나타내는 방법에 1을 더하면 2를 만들 수 있다. 👉 1 + 1 (1가지)
- 2를 사용하여 2를 만들 수 있다. 👉 2 (1가지)
- 3 를 1, 2, 3의 합으로 나타내는 방법의 수 = 3, 1 + 1 + 1, 2 + 1, 1 + 2 (4가지)
- 2를 만드는 방법들에 1을 더하면 3을 만들 수 있다. 👉 1 + 1 + 1, 2 + 1 (2가지)
- 1을 만드는 방법들에 2을 더하면 3을 만들 수 있다. 👉 1 + 2 (1가지)
- 3을 사용하여 3을 만들 수 있다. 👉 3 (1가지)
- 4 를 1, 2, 3의 합으로 나타내는 방법의 수
- 3을 만드는 방법들에 1을 더하면 4을 만들 수 있다.
👉 1 + 1 + 1 + 1, 2 + 1 + 1, 3 + 1, 1 + 2 + 1 (4가지) - 2을 만드는 방법들에 2을 더하면 4을 만들 수 있다.
👉 1 + 1 + 2 , 2 + 2 (2가지) - 1을 만드는 방법들에 3을 더하면 4을 만들 수 있다.
👉 1 + 3 (1가지) - →→ 4 + 2 + 1 = 7가지
- 3을 만드는 방법들에 1을 더하면 4을 만들 수 있다.
🤔 슬슬 규칙이 보이지 않나용
n에서 1을 뺀 수에 1을 더하는 방법
+
n에서 2을 뺀 수에 2을 더하는 방법
+
n에서 3을 뺀 수에 3을 더하는 방법
=
n을 1, 2, 3의 수의 합으로 나타낸 방법!
마찬가지로 5 를 1, 2, 3의 합으로 나타내는 방법의 수를 구하려면
- 4를 1, 2, 3의 합으로 나타내는 방법의 수에 1을 더하거나
- 4를 만드는 방법에 1을 더하는 경우의 수
👉 1 + 1 + 1 + 1 + 1, 2 + 1 + 1 + 1, 3 + 1 + 1, 1 + 2 + 1 + 1, 1 + 1 + 2 + 1, 2 + 2 + 1, 1 + 3 + 1
= 7가지
- 4를 만드는 방법에 1을 더하는 경우의 수
- 3을 1, 2, 3의 합으로 나타내는 방법의 수에 2를 더하거나
- 3를 만드는 방법에 2를 더하는 경우의 수
👉 3 +2, 1 + 1 + 1 +2, 2 + 1, 1 + 2 +2
= 4가지
- 3를 만드는 방법에 2를 더하는 경우의 수
- 2를 1, 2, 3의 합으로 나타내는 방법의 수에 3를 더하면, 5 를 1, 2, 3의 합으로 나타내는 방법의 수를 모두 구할 수 있다.
- 2를 만드는 방법에 3을 더하는 경우의 수
👉 1 + 1 + 3, 2 + 3
= 2가지
💡 7 + 4 + 2 = 총 13가지
- 2를 만드는 방법에 3을 더하는 경우의 수
따라서 DP로 풀수 있는 문제이다.
점화식
$$ dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] $$
→ dp 배열에 1 ~ n 까지의 수의 1,2,3의 합으로 나타낼 수 있는 방법의 수를 저장하여 참조한다.
소스
import sys
t = int(sys.stdin.readline().rstrip())
dp = [0] * 11
dp[1] = 1
dp[2] = 2
dp[3] = 4
for _ in range(t):
n = int(sys.stdin.readline().rstrip())
if dp[n] == 0:
for i in range(4, n + 1):
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
print(dp[n])'알고리즘' 카테고리의 다른 글
| [Python] 백준 5430 AC_문자열과 deque (0) | 2023.03.28 |
|---|---|
| [Python] 백준 6064_카잉달력 (최소공배수 활용) (0) | 2023.03.26 |
| [Python] 프로그래머스 레벨2 - 혼자서 하는 틱택토 (1) | 2023.02.25 |
| [Python] 백준 16139번 : 인간-컴퓨터 상호작용 (0) | 2023.02.11 |
| [Python] 백준 14889_스타트와 링크 (0) | 2023.02.10 |